We Love Physics

We love physics:
1)Το τριγωνάκι για τα κάλαντα   

Χρησιμοποιώντας  σκληρό ισοπαχές σύρμα φτιάχνουμε ένα τριγωνάκι με ίσες πλευρές σαν αυτό που έχουν  τα παιδιά για τα κάλαντα .

            

                

Α. Αν είναι m η μάζα κάθε πλευράς του τριγώνου και α το μήκος της, με ποιο από τα παρακάτω συμφωνείτε;

η  ροπή αδράνειας του τριγώνου ως προς άξονα z που περνάει από το σημείο τομής των διαμέσων και είναι κάθετος στο επίπεδο είναι      α. ίση με ¹/₃ ma²      

β. ίση με ¼ ma² 

γ. Μεγαλύτερη από τη ροπή αδράνειας ως προς άξονα παράλληλο προς τον z και διερχόμενο από μια κορυφή του τριγώνου      

δ. ίση  με ½ ma²

Β. Κρεμάμε το μάζας 3m τριγωνάκι από οριζόντιο καρφί από την κορυφή Α,  έτσι ώστε η πλευρά ΒΓ να είναι οριζόντια. Με τη δράση μιας ώθησης παράλληλης προς την ΒΓ σπρώχνουμε το τριγωνάκι ώστε να ξεκινήσει να στρέφεται με γωνιακή ταχύτητα ω.

Πόση πρέπει να είναι η τιμή της ω ώστε να στραφεί κατά 90⁰, έτσι ώστε κατά τη στιγμή που θα φθάσει στο ανώτερο ύψος,

με μηδενική γωνιακή ταχύτητα,  η πλευρά ΒΓ να είναι κατακόρυφη.
 
2)Η απερίγραπτη κίνηση της ράβδου.

Μια ομογενής ράβδος έχει μάζα 200 g, μήκος 30 cm  και αρχικώς ακινητεί σε λείο οριζόντιο τραπέζι. Σε κάποια στιγμή χτυπιέται κάθετα από μία οριζόντια δύναμη σε σημείο που απέχει 10 cm από το μέσον της και της μεταβιβάζεται ορμή 3 Ns. Να περιγράψετε την κίνηση που θα επακολουθήσει.

3)Ο σωλήνας μπορεί και να ανατραπεί;

Καθεμιά από τις δύο όμοιες ομογενείς σφαίρες έχει μάζα m  και ακτίνα  r. Ο ομογενής κυλινδρικός σωλήνας μέσα στον οποίο βρίσκονται ανοικτός και από τα δύο άκρα έχει μάζα Μ και ακτίνα R . Το σύστημα βρίσκεται σε οριζόντιο επίπεδο.   Να υπολογίσετε τον λόγο των μαζών m/M  ώστε ο κυλινδρικός σωλήνας με τις δύο σφαίρες να  ανατραπεί. Δίνεται R= 7r/4

4)Το βλήμα  και η ξύλινη σφαίρα.      

Ένα βλήμα μάζας m κινούμενο με οριζόντια ταχύτητα υ₀ στο ενσφηνώνεται σε αρχικά ακίνητη ξύλινη σφαίρα  μάζας Μ και ακτίνας R η οποία ισορροπεί σε οριζόντιο επίπεδο. Η ταχύτητα του βλήματος πριν την ενσφήνωση βρίσκεται στο κατακόρυφο επίπεδο που περνάει από το κέντρο της σφαίρας και η  ενσφήνωση γίνεται σε ύψος h = ½R από το έδαφος.  Να προσδιορίσετε τα βασικά στοιχεία της κίνησης της σφαίρας με το ενσωματωμένο βλήμα μετά την ενσφήνωση.  Οι τριβές θεωρούνται αμελητέες. 

Να θεωρήσετε ότι η μάζα του βλήματος , συγκρινόμενη με τη μάζα της σφαίρας, είναι αμελητέα και ότι το βλήμα είναι  σημειακό αντικείμενο.


5)Το μισό καρπούζι              

Το σφαιρικό καρπούζι έχει κοπεί στη μέση. Το μισό  βρίσκεται σε οριζόντιο τραπέζι με το διαμετρικό του «κόκκινο» επίπεδο κατακόρυφο. Το αντικείμενο αφήνεται ελεύθερο και αρχίζει να πέφτει κυλιόμενο

χωρίς να ολισθαίνει προς τα δεξιά. Να υπολογίσετε τη δύναμη που ασκεί το καρπούζι στο τραπέζι κατά τη στιγμή που το διαμετρικό του επίπεδο (που έχει χρώμα κόκκινο ) γίνεται οριζόντιο.

Το αντικείμενο (μισό καρπούζι)  να θεωρηθεί ημισφαίριο μάζας m και ακτίνας R η ροπή αδράνειας του οποίου ως προς άξονα διερχόμενο από  το διαμετρικό επίπεδο και από το κέντρο του κύκλου Ο είναι 2mR²/5. Το κέντρο μάζας του ημισφαιρίου βρίσκεται στον άξονα συμμετρίας σε απόσταση 3R/8 από το διαμετρικό επίπεδο. Όταν το διαμετρικό επίπεδο γίνεται οριζόντιο η ακτίνα της τροχιάς του κέντρου μάζας να θεωρηθεί ίση με r

.6)Μετρώντας ενέργεια με ζυγό και με μεζούρα 

Ένας ομογενής επίπεδος δίσκος ακτίνας R διατηρείται κατακόρυφος στρεφόμενος γύρω από ακλόνητο οριζόντιο άξονα που περνάει από το κέντρο του. Ένα κομματάκι μάζας m – θεωρούμενο  σημειακό αντικείμενο-  αποσπάται από την άκρη του δίσκου σε μια τέτοια στιγμή και σε μια τέτοια θέση ώστε στη συνέχεια - μετά δηλαδή την εκτόξευσή του- να κινηθεί κατακόρυφα προς τα πάνω στην κατακόρυφο του σημείου από το οποίο κόπηκε. Το μάζας m αυτό κομματάκι φθάνει σε ύψος Η και αρχίζει να πέφτει. Μετράμε με τη μετροταινία το ύψος Η και την ακτίνα του δίσκου και με ζυγό τη μάζα Μ του δίσκου και τη μάζα m του κομματιού που αποσπάστηκε. Βασιζόμενοι στις μετρήσεις και σε φυσικούς νόμους  υπολογίζουμε την κινητική ενέργεια του δίσκου πριν και μετά την  απόσπαση. Πώς το καταφέρνουμε; Το κομματάκι που αποσπάστηκε θεωρείται σημειακό αντικείμενο.

7)Αν το βαρίδι είναι αρκετά βαρύ.     

Ένα αντικείμενο σαν λεκάνη βρίσκεται σε οριζόντιο τραπέζι και έχει μια σφαιρική κοιλότητα ακτίνας R και βάθους h και ακτίνας R. Μέσα στη σφαιρική αυτή κοιλότητα τοποθετούμε μία ομογενή σφαίρα ακτίνας R και μάζας m . Το αντικείμενο – λεκάνη έχει μάζα Μ και συνδέεται με νήμα μέσω τροχαλίας με ένα μικρό βαρίδι .

Σας ζητούμε βασιζόμενοι σε φυσικούς νόμους να προβλέψετε την τιμή της ελάχιστης μάζας που πρέπει να έχει το βαρίδι ώστε η σφαίρα να εξέλθει από την κοιλότητα.

8)Το δακτυλίδι καθυστερεί.                   

Ένας κύλινδρος και ένας δακτύλιος ίσων ακτίνων βρίσκονται σε επαφή σε κεκλιμένο επίπεδο γωνίας θ και συγκρατούνται. Τα δύο σώματα αφήνονται ταυτόχρονα και κυλίονται στην επιφάνεια του κεκλιμένου επιπέδου χωρίς να ολισθαίνουν. Πόσο θα απέχουν τα δύο κέντρα μάζας των δύο σωμάτων μετά από ένα δευτερόλεπτο; Τα σώματα είναι ομογενή.       Απ: 41,7 c m.

9)Οι ποδηλάτισσες  
"Ευρείς λεωφόρους διασχίζουν φευγαλέα οι ποδηλάτισσες "             
                              Οδυσσέας Ελύτης

         Το ομώνυμο μυθιστόρημα της Ρέας Σταθοπούλου αρχίζει με τον στίχο του Οδυσσέα Ελύτη για τις ποδηλάτισσες. Όσο για μας τους γένους αρσενικού είναι γεγονός ότι το «μαγικό» αυτό δίτροχο του εφηβικού μας σύμπαντος  μάς προκαλούσε δέος. Όταν δεν έτρεχε έπεφτε και δεν έπεφτε μόνο όταν το κέντρο μάζας του είχε μια  ταχύτητα αξιοπρεπή. Ανεξήγητο για όποιον δεν έχει  συναντηθεί με τη Φυσική ή ξέρει μόνο από Μηχανική του υλικού σημείου. Δύο είναι οι βασικές  έννοιες με τις οποίες χρειάζεται να είναι εξοικειωμένος,  η στροφορμή και η ροπή και οι δύο μεγέθη διανυσματικά πράγμα που σημαίνει ότι για να κατανοήσει κανείς τις παραξενιές του ποδηλάτου πρέπει να διαθέτει και κάποια χωρική νοημοσύνη,   spatial intelligence όπως τη  λέει  ο Gardner. Η μεταβολή της στροφορμής ( ως προς κάποιο σημείο ) είναι ίση με την ώθηση της συνολικής ροπής (ως προς το ίδιο σημείο) μας λέει η Μηχανική του rigid body.

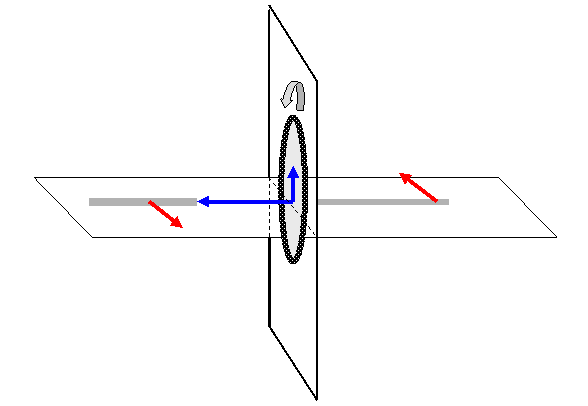
Αν φανταστούμε ένα τροχό ποδηλάτου ακίνητο με τον άξονά της περιστροφής του οριζόντιο. Αν ασκήσουμε μια δύναμη στον άξονα θα τον δούμε να στρέφεται απολύτως αναμενόμενα. Αν όμως έχουμε θέσει σε περιστροφή τον τροχό ΜΕ ΤΟΝ ΑΞΟΝΑ ΟΡΙΖΟΝΤΙΟ και ασκήσουμε στον άξονα μια δύναμη ΚΑΤΑΚΟΡΥΦΗ αυτό που θα συμβεί θα μας εντυπωσιάσει. Ο άξονας του τροχού ΘΑ ΣΤΡΑΦΕΙ ΣΕ ΟΡΙΖΟΝΤΙΟ ΕΠΙΠΕΔΟ. Και οι φυσικοί το αιτιολογούν με βάση τις γεωμετρικές ιδιαιτερότητες της

ροπής. Πώς ακριβώς;

Εφόσον το ποδήλατο είναι ακίνητο και το αφήσουμε θα ανατραπεί. Η ροπή του βάρους  λένε οι φυσικοί. Εάν όμως βρίσκεται σε κίνηση έχει ήδη στροφορμή και -εφόσον γύρει- η ροπή του «κατακόρυφου»

βάρους προσθέτει οριζόντια στροφορμή στην ήδη υπάρχουσα.

Πώς θα μπορούσαμε να κάνουμε ένα σχήμα και να τα παραστήσουμε  όλα αυτά την οριζόντια δηλαδή στροφορμή του τροχού κάθετα στην κίνηση και την οριζόντια -κατά τη διεύθυνση της κίνησης- στροφορμή η οποία προστίθεται διανυσματικά στην αρχική